A New Historical Solar Eclipse Discovered for Calculating Delta T

Abstract

This work presents a revised long‑term model for ΔT based on a hyperbolic formulation that more accurately captures Earth’s rotational deceleration over the early Holocene. Using NASA positional data, the ΔT values for the Perinos and Zhenxun eclipses were calculated with corrected Pc Allakka coordinates, while the remaining ancient eclipse values were taken from Stephenson et al. and incorporated into a unified dataset for model fitting. The combined data reveal systematic deviations from the standard polynomial approximations, particularly before ~2000 BC, where quadratic models consistently overestimate ΔT and fail to reproduce the observationally constrained eclipse paths.

The proposed hyperbolic model is motivated by the physical expectation that Earth’s rotational slowdown does not follow a constant or smoothly varying quadratic trend, but instead approaches an asymptotic limit governed by tidal dissipation, long‑term oceanic mass redistribution, and secular changes in Earth’s moment of inertia following deglaciation. When fitted to the full ancient eclipse dataset, the hyperbolic curve yields a coherent, monotonic trend that passes through both the well‑established historical eclipses (e.g., Zhenxun 2136 BC) and the newly identified candidate annular eclipse at Perinos (Lake Onega) around 4261 BC. The latter aligns with the model without requiring ad‑hoc adjustments, supporting its plausibility as a genuine observational record.

These results indicate that ΔT over multi‑millennial timescales is better represented by a hyperbolic decay function than by traditional parabolic approximations. The model provides a physically grounded and empirically consistent framework for reconstructing ancient eclipse visibility and for interpreting archaeological or palaeoastronomical records that may encode observations of solar phenomena.

____

Aloitin komiasti Englannin kielellä jotta ulkomaillakin ymmärtävät mistä täällä puhutaan. Edellisen blokkauksen jälkeen olen nyt entistä varmempi, että Äänisen rannan kalliopiirrokset todella ovat merkintöjä siellä nähdyistä auringonpimennyksistä. Onnistuin parantamaan Pc Allakan tarkkuutta ja  NASAn sivustoilta löytyy nykyään myös koordinaatit,  joista  sen paikoille voi laskea  tapauskohtaiset korjaustermit. Termien avulla ohjelman tarkkuus pysyy hyvänä  ainakin muutaman päivän ajan. Näillä eväillä tulosten pitäisi nyt olla tarkkoja. Epävarmuutta niihin tuo enää maapallon pyörimisnopeuden vaihtelu, koska muita yhtä vanhoja havaintoja, joihin tulosta voisi verrata, ei maailmassa vielä ole.

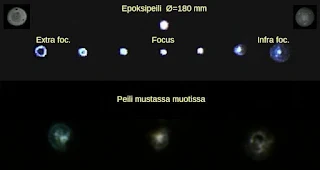
Kuten edellisellä kerralla jo kerroin, Perinosin alueella on näkynyt useita auringonpimennyksiä 6000 vuotta sitten, monet niistä myös rengasmaisia. Tarkistuslaskennassa selvisi, että ainakin vuoden -4260 pimennys olisi tosiaan näkynyt siellä (61.677N, 36.032E). Kuva siitä alla.

Kuva 1. Pc Allakan käsitys Perinosin pimennyksestä vuonna 4261 BC.

Laskennallisesti kuvan tilanne olisi näkynyt 56° astetta Perinosista länteen mutta menneisyydessä maa on pyörinyt nopeammin ja Perinos on ehtinyt lasketulle paikalla. 

Vaikka hidastuminen on vähäistä on sen kasautuva vaikutus maakellon lukemaan suuri. Tässä tapauksessa "virhe" on  ainakin 13403 sek. mutta yhtä hyvin se voisi olla montakin 24 tunnin monikertaa suurempi. Kuvan arvo 186203 sek = 13403+2*24h.

Virhettä kutsutaan Delta T:ksi,  Nasan  sivustoilla  sen laskemiseen on tarjolla jopa 13 erilaista kaavaa, kukin omalle aikajanalleen  sovitettuna.  Jos pyritään sekuntien tarkkuuksiin tämä voikin olla tarpeen mutta eihän meillä vanhoista  pimennyksistä näin tarkkoja tietoja ole. Kyllä niille vähempikin tarkkuus riittäisi, uskon. Eivätkä nuo Nasankaan kaavat kiveen hakattuja ole. On niilläkin virherajansa ja niiden sisään mahtuisi helposti montakin erilaista kaavaa, joista kukin  korvaisi nuo Nasan kaikki. Edellisessä blokkauksessa esitin jo yhden malliksi. Jatkan nyt siitä.

Teoreettisesti pyörimisen hidastuminen tuottaa maakellon lukemaan virheen, joka kasvaa parabolisesti, jos hidastuminen on tasaista. Näin ei kuitenkaan ole, lyhytaikaista muutosta aiheuttaa myös vuodenaikojen vaihtelu, lumipeitteen sijainti ja jopa matala- ja korkeapainealueiden liikkeet. Monissa tutkimuksissa on kuitenkin havaittu, että mukana on pakko olla myös muita pitkäkestoisia ilmiöitä, jotka vaikuttavat satojen, ellei jopa tuhansien vuosien ajan. Itse uskon, että ilmiön taustalla on jääkauden jälkeisten napa-alueiden sulaminen. Se oli aluksi nopeaa, kun jäätä oli paljon ja ilmasto lämmin. Myöhemmin sulaminen hidastui kunnes pikkujääkauden jälkeen jäätiköt jälleen alkoivat kasvaa.

Jos oletamme,  että hidastumisen muutos on ollut ajan suhteen lineaarista,  hid. = f+gt,  voimme integroimalla laskea 

(1)                       ΔT =36525 ∫t(f + gt/2)dt  = 36525 (ft²/2 + gt³/6) + C.

Kaavassa ajan yksikkönä  on juliaaninen vuosisata mistä johtuu tuo kerroin 36525 eli päivien luku tuossa ajassa. Pc Allakassa  ajan alkuhetkenä on vuosi 1900 ja siinä  kaavan 1 kertoimet on ratkaistu suuresta joukosta havaintoja, joista vanhin on PeriNos. Muut havainnot ovat F. R. Stephenson et al tutkimuksesta, koska uskon siinä olevan mukana kaikki ne alkuperäiset havainnot, joiden perusteella Nasakin on omat kaavansa laatinut (kuva). Halusin myös nähdä, millaisen käyrän aineisto tuottaisi, jos sen etsijällä ei olisi ennakkoon käsitystä toivotusta tuloksesta (parabeli). 

Ja toden totta, omakin analyysini tuotti heti omaa odotustani vastaavan hyperbelin;) Ja osui sitäpaitsi hyvin lähelle kuvan 1 arvojakin,  jopa hiuksenhienosti paremmalla korrelaatiolla  kuin parabeli.  Alla oma analyysini aineistosta. 

Kuva 2.  Maakellon virhe vuosina 4261 CB - 1500 AD
Kuvan  arvot keltaiselle käyrälle. Punaisen käyrän arvot ovat 
a=539.33829 b=4.3314899 c=-1.0886124

Stephensonin aineiston lisäksi siinä oli mukana myös omat laskuni PeriNosin pimennyksestä sekä  kontrollina  vuoden -2136 Zhenxunin pimenys. Analyysin tulos osoittaa nyt lopullisesti, että  Perinosin rantaan hakattu kalliopiirros  voisi olla merkintä siellä nähdystä pimennyksestä vuonna 4261 BC.  Arvolla  ΔT=13403s+3*24h pimennys osuisi myös samalle Delta T:n muutosta kuvaavalle käyrälle kuin  Zhenxunin pimennys ja tukisi samalla myös tämän havainnon aitoutta. 

Vaikeutena on ollut, ettei Zhenxunin havainnon tarkka leveysaste ole tiedossa. On jopa spekuloitu, ettei sitä siellä olisi nähty täydellisenä lainkaan. Laskin siksi ΔT:n arvot sinne kahdelle leveysasteelle, 36°N ja 39°N, ja molemmissa pimennys olisi tosiaan näkynyt, Pc Allakan mukaan  rengasmaisena aivan kuten Perinos kuvassa 1. Tämä on mielenkiintoinen yksityiskohta. Kyseessähän on tuo kuuluisa pimennys, jossa Keisarin astrologit menettivät päänsä, kun  pimennyksen aikana olivat nukkuneet rapulaisina, eivätkä olleet  varoittamassa tapahtumasta. Pimennys oli siksi saanut kuuluisuutta ja tullut muistiinmerkityksi, missä sitä oli kuvailtu harmonisesti epätäydellisenä (eivät kohdanneet harmonisesti) Tämä on saanut monet päättelemään, ettei se ollut täydellinen mutta kyllä minusta rengasmainenkin  voisi  epäharmonisesta käydä - vaikka  enhän minä Kiinan kielestä mitään ymmärrä. 

Analyysin tuloksena saamme nyt kuvan 2 arvoilla ja kaavalla 1 laskien  pyörimisen  hidastumisen arvoiksi vuonna 1900

 (2)                f=2b/36525=1.065 ms/cy  ja   g=6c/36525= -0.083 ms/cy²

jolloin ajanlaskun alussa  olisi ollut   f=1,065 - 19g = 2.64 ms/cy.

Vastaavasti kuvan punaisen käyrän arvoilla  olisi f vuonna 1900 ollut 0.24 ms/cy ja ajanlaskun alussa  3.63 ms/cv. Tämä hieman arveluttaa, näillä arvoilla hidastuminen olisi vuonna 2032 jo kokonaan loppunut. Vaikka onhan tuota mediakin jo viime vuosina alkanut ihmetellä. Miksi pyörimisnopeus kiihtyy jo nyt vaikka ilmastonmuutoksen piti sitä hidastaa?

Analyysin tuottama  muutos g kaavassa 1 on kertaluvultaan samaa luokkaa, mitä napajäätikoiden sulaminen aiheuttaisi, jos merenpinta sen seurauksena nousisi 10 mm. Olen tuon itsekin joskus laskenut mutta Munk ja Revelle tekivät sen jo vuonna 1952. Heidän mukaansa 10 mm:n nousu pidentäisi päivän pituutta 0.06 ms eikä tuota  kukaan vielä ole myöhemmin kiistänyt eikä sitä tämäkään blokkaus tee.  

Linkkejä

1  Nasan delta T laskukaavat
2  Historical values of the Earth's clock error ΔT and the calculation of eclipses  

3  Measurement of the Earth's rotation: 720 BC to AD 2015 

4 Astronomical Dating of Babylobian Texts Describing the Total Solar Ecclipse...

5 Five Millenium Canon of Solar Eclipses Database

6 Sea Level and the Rotation of the Earth

7 Wikipedia Post-Gglasial See Level Rise

8 Nasa Horizons System

Vanhaa kamaa

Osui kesän aikana eteen vanha tuttu Wolmari Isopaljo, armoitettu tarinan kertoja ja hyvä ystävä. Kertoi kirjoittavansa tarinaa netin salaliittoteorioista ja tausta-aineistoon perehtyessään oli törmännyt enkelin kuvaan Äänisen rannan kalliopiirroksissa, UNESCOn maailmanperintökohteessa Site 1070 - RUS.  Nettihän on täynnä vanhoja enkelitarinoita, joissa muinaiset alienit ovat käyneet maassa opastamassa alkuasukkaita. Kaivoi  kuoma innoissaan kännyä ja kysyi mielipidettä. 

Kertoi piirroksen  olevan Äänisen itärannan pirunnokalta ja veti varmemman vakuudeksi esiin vielä  linkin, jossa alue esiteltiin. Kun en tarpeeksi innostunut, pääsi lopulta varsinaiseen asiaan. Alueellahan myös on useita aurinkoa ja kuuta esittäviä piirroksia, joiden merkitystä arkeologit ovat kilvan ihmetelleet. Wolmari päästi röhönaurun ja kertoi kuinka typeriä teorioita oli esitetty vaikka kuvat ihan ilmiselvästi esittivät vain tavallisia  auringonpimennyksiä, osittaisia ja täydellisiä, yksi jopa rengasmaista.

Ja toden totta, jo piti vanhan jääränkin yhtyä Wolmarin ilonpitoon. Miksi noin selvää yhteyttä ei  aikaisemmin ole huomattu. Jalkojakin oli kuviteltu vain auringon säteiksi vaikka eihän se aurinko ilman jalkoja olisi entisaikaan osannut edes taivaalla  kulkea.

Tietojen mukaan piirrokset ovat vuosilta 5000 - 4000 eKr. ja Wolmarin pyynnöstä otin työkseni selvittää, olisiko tuona ajanjaksona voitu alueella nähdä kuvan kaltaista rengasmaista pimennystä. Wolmari tiesi, että nuorena miehenä olin laatinut ohjelman PcAllakka, joka oli jopa julkaistu.  Vaadittu aikaskaala tosin oli reilusti yli ohjelman lupaaman tarkkuusalueen mutta pienin varauksin aloin kuitenkin hakea ja löytyihän niitä, jopa kolme kappaletta. Alla kuva vanhimmasta niistä

Toinen tällä alueella näkynyt rengasmainen pimennys on ollut 4261 kesäk. 17 eKR ja kolmas

19. heinäk. 4234 eKr. Samalta sataluvulta löytyi  vielä  13 kpl  yli 40% pimennystä  ja pienempiä pilvin pimein mutta muita rengasmaisia ei haaviin tarttunut, ei vaikka laajensin hakualuettakin molempiin suuntiin. PcAllakan kuvat näistä isoista on tuolla.

Totuuden nimessä on kuitenkin sanottava, että korjasin tuota kuvassa näkyvän dT:n kaavaa hieman. NASAn kaavoilla  sen arvo olisi ollut 118974 sek. Ero on suuri, koska aikaskaalakin on suuri. Tuo  Delta T tarkoittaa maapallon pyörimisen hidastumisesta aiheutuvaa virhettä pimennyksen näkymisalueen pituusasteessa. Jos katsomme menneisyyteen, maa on silloin pyörinyt nopeammin ja laskettu paikka on ehtinyt alta pois. Hidastumiseksi NASA on olettanut  n. 0.0017 sek/vuosisata,  PcAllakassa sen korjattu arvo on n. 0.0023 sek./vuosisata. Molemmat ovat pieniä  mutta, kun ne tuhansien vuosien aikana vaikuttavat joka päivä ja kasvattavat virhettä korkoa korolle periaatteella, on tulos sitten tuo minkä alla olevasta kuvasta näemme. Vuoden 4279 kesäk. 7 eKr oli Delta T jo 140637s =1pv 15h 3m 57s.

Kuvassa punainen käyrä esittää Delta T:n muutosta NASAn arvoilla laskettuna, keltainen on PcAllakan uusitun kaavan tuottama tulos.  Siinä NASA arvojen lisäksi  on käytetty kaikkia ennen ajanlaskun alkua löytyneitä historiallisia pimennyksiä ja laskettu niille uudet Delta T:n arvot. Alla taulukko niistä. 

      Paikka     Aika       Pituus    Leveys   Delta T

   Peri Nos -4278*6*7    E  36.02  N 61.41  140637 sek.

   Peri Nos -4260*6*17   E  36.02  N 61.41  139622

   Peri Nos -4233*7*19   E  36.02  N 61.41  138106

   Zhenxun  -2136*10*22  E 112.68  N 36.00   50029 

   Ugarit   -1374*5*3    E  35.78  N 35.60   30582

   Anatolia -1311*6*24   E  35.00  N 39.00   29225  

   Chufu     -708*7*17   E 117.00  N 35.65   18088

   Xian      -180*3*4    E 108.90  N 34.30   10835  

   Babylon   -135*4*15   E  44.42  N 32.54   10316

PS.

PcAllakan taival alkoi vuonna 1987, jolloin Toptronics osti 4 kpl sen Amstrad kotimikrolle laadittuja ohjelmalevykkeitä. Vuonna 1990 WEILIN+GÖÖS tuli mukaan ja antoi sysäyksen laatia ohjelmasta myös PC-koneissa toimiva versio, Versio n:o 1.10. Ohjelman kaupallinen tarina päättyi tähän mutta omaan käyttöön sen koodia on ajoittain muokattu. Nykyinen versionumero on 4.0. Valitettavasti se toimii enää vain DOS Boxin kanssa mutta on silti nykyäänkin vielä paljon nopeampi kuin alkuvuosinaan sen aikaisissa koneissa.  Vanhassa kotimikrossa uuden paikan lasku kesti yli 30 s mikä nykyään tapahtuu sekunnin murto-osissa. Alla vielä kuva vanhasta Ammusta ja sen käsitys tuosta em. Babylonin pimennyksestä.

Hyvin vaan pelittää vanha Ammu vaikka onkin jo pölyn peitossa.

Lisää kuvia ja linkkejä täällä

Kännyn telejatko 5€

Kas, tupsahti nettiä selatessa tuollainen eteen.

Ei ollut hinnalla pilattu ja alkoi kiinnostaa, kun kiikarilla katselu on karsastuksen vuoksi käynyt ikääntyessä hankalaksi. Euron lisähinnalla vekottimeen sai vielä telineen, jonka avulla sen voi kiinnittää vaikka telejatkeeksi kännykkään. Paljoa en tuotteelta odottanut mutta teline kiinnosti ja sen avulla saisi ainakin kännykän kiinni kamerajalustaan, joten otin riskin ja tein tilauksen enkä ole katunut.

Tarjottu monokulaari on paljon pienempi kuin tavallinen kiikari, jota  kuitenkin joutuisin itse  käyttämään toinen silmä kiinni. Tilaamani yksilö painaa vaivaiset 38g ja mahtuu vaikka nyrkkiin, jolloin sitä mukava käyttää vaikka pidempikin tovi. Päiväkäyttöön objektiivin kokokin on ihan riittävä eikä tuo tarpeetonta painoa katseluun.  Sen laatu voisi kyllä olla parempi, omassani on pientä värivirhettä, mutta paljain silmin sitä tuskin huomaa. Valokuvissa virhe kyllä erottuu mutta ei kovin pahasti. Arvioikaa itse. Alla kuva omalta takapihalta 6 metrin etäisyydeltä sekä osasuurennus siitä samaan kokoon kuin samalta paikalta telejatkeella kuvatun otos. Pikselien määrä kaikissa kuvissa on sama. 

Tiainen kuvattuna telejatkeella ja ilman

Ohessa kuva monokulaarista kännykkään ja jalustaan kiinnitettynä. Jalustan käyttö oli pakko, ilman sitä hommasta ei tullut yhtään mitään. Kameran oma optinen zoomi on nelinkertainen ja, jos sen päälle  asettaa vielä 8 kertaisen telejatkeen, ei kenenkään käsi ole kyllin vakaa onnistuneen kuvan ottamiseen. Oma kännyni ei käsivaralta osannut edes tarkentaa ja laukaisunapin hipaisukin täristi kuvaa niin, että  katsoin suosiolla myös ajastimen käytön pakolliseksi.

Kännykkäteline on muutoin asiallinen mutta jalustaan sitä ei telejatkeen kanssa saa kiinni. Sitä varten piti väsätä ja liimata oma lisäosa,  jonka turvaksi ja kaunistukseksi laitoin vielä  mustan ilmastointiteipin. Ensimmäinen yritys ilman liimausta petti ja känny putosi lattialle.  Nyt teline toimii ja soveltuu max 10 mm vahvalle ja 63-78 mm leveälle kännykälle. 

Telejatkeen sijoittelussa kameran eteen pitää kyllä olla tarkkana. Jos se on vähänkin sivussa, näkyy se heti kuvassa. Ei välttämättä kuvaustilanteessa mutta valmiissa kuvassa virhe aiheuttaa epäterävyyttä kuvan eri osiin. 

Ohessa vielä pari testikuvaa taivaalta.

Bongaa Paavo Nurmi

Selasin tuossa Tähdet ja Taivas lehden uusinta numeroa ja hämmästelin  taas - mm. miten hienoja kuvia harrastajavälineilläkin  nykyään saa otettua. Kuvan pääsy lehden sivuille on tietysti harrastajalle iso juttu mutta entäs sitten? Kuvan ottoon ja sen käsittelyyn on uhrattu paljon aikaa, hetken se  saa loistaa lukijoiden silmissä mutta vajoaa sitten taas pian historian roskatynnyriin. 

Kuinka moni meistä nykyään katseleekaan enää Tähdet ja Avaruus lehden vanhoja vuosikertoja ja ihastelee niiden sivuilta löytyviä hienoja kuvia?  Jos jotain tiettyä  taivaankannen kohtaa haluaisikin tarkastella, löytyy se  paljon  nopeammin  GoogleSky:sta. 

Siksi hyvät harrastajat,  haastan teidät ottamaan seuraavan askeleen ja nostamaan harrastuksenne uudelle tasolle. Bongatkaa Paavo Nurmi, kuvatkaa ja mitatkaa se ja lähettäkää tuloksenne kansainvälisen tiedeyhteisön käyttöön pikkuplaneettojen ratoja laskettaessa.

"Taidekuviin" verrattuna planeettakuvaus on sitä paitsi paljon helpompaa. Kuvaa ei tarvitse käsitellä. Riittää, että kohteen saa näkyville ja laittaa kuvanoton tarkan ajankohdan muistiin. Sekunnin tarkkuus riittää ja hitaasti liikkuvien kohteiden osalla vähempikin. Eikä paikan mittaus nykytekniikalla ole temppu eikä mikään (sigh, toista se ole ennen).  Visuaalisesti paikan voi  usein lukea suoraan kartalta tai tarkkusmittauksissa oma kuva luetaan mittausohjelmaan, jossa  kohteen ympäriltä valitaan kolme vertaustähteä ja annetaan ohjelman hoitaa homma. Kuva tuossa alla. (Laajakenttäisissä kameroissa tilanne on toinen mutta ei kovin pahasti.)

Kuva 1. ScanIt ja akselien mittakaavan asetus

Omassa käytössäni on ollut ohjelma nimeltä ScanIt joka on ladattavissa tuolta. Muitakin varmaan löytyisi mutta tämä oli ilmainen ja sillä voi tehdä paljon muutakin. 

Kuvassa 1 ohjelman työtilaan on "repäisty" kappale Orionin tähdistöä GoogleSky:sta. Kuvan mittakaava asetetaan antamalla  sen kolmelle pisteelle halutut koordinaatit, tässä tapauksessa  tähtien rektaskensiot ja deklinaatiot. Sen jälkeen minkä tahansa pisteen koordinaatit voi lukea klikkaamalla sitä hiiren kursorilla. Kursorin osoittama alue näkyy sivuikkunassa zoomattuna, minkä avulla kohdistuksen voi tehdä  pixelin tarkkuudella tarkasti. Jos tuntuu, ettei tämä ole riittävä, kuten kuvassa 1, kannattaa kuvaa  suurentaa  ennen mittausta.

Kuvassa kolmioilla merkityt kohteet ovat vertaustähtiä, joiden avulla mittakaava on asetettu. Nekin voi lukea GoogleSky:sta, jos kuvan alueelta ei muuta tarkemmin tunnettua tähteä löydy. Tämä on yleinen ongelma harrastajaputkissa, joissa näkökenttä on pieni. Onneksi GoogleSky näyttää olevan jopa yllättävän tarkka.  Alla osasuurennus kuvasta 1, johon on liitetty GoogleSky:n kämmenellä osoittamat koordinaatit. (Kämmen on vähän karkea osoitin tarkkaan mittaukseen mutta onneksi kuvaa saattoi Zoomata.)

Kuva 2. GoogleSky:n koordinaatit merkityille tähdille.

Netistä tähtien tarkkoja koordinaatteja voi etsiä  esim. tuolta, mistä niitä on helppo valita ja siirtää jatkokäsittelyyn omalle koneelle. Alla luettelo kuvan 1. alueelta löytyneistä tähdistä. Tuossa vielä toinen linkki, mistä tähtiä löytyy enemmän ja niitä voi katsella myös kartalla, jolta mitattavan kohteen paikankin voi arvioida melko tarkasti jopa ilman mittausta.

Näemme, että GoogleSky:n arvot ovat hyvin lähellä SAO luettelon arvoja.  Vertailun vuoksi tuossa alla ovat myös omat testimittaukseni tulokset. Mittausta häiritsi testikuvan suuri pixelikoko mutta muutoin tulos oli kyllä ihan tyydyttävä, vain kakkoskohteen RA:n yli 4 kaarisekunnin virhe olisi tositilanteessa vaatinut tarkistusmittauksen, vaikka niinhän tositilanteessa muutoinkin on aina meneteltävä. Varsinaisen kohteen lisäksi silloin on aina syytä mitata myös jokunen tunnettu kohde, jotta nähdään, onko vertaustähtien koordinaatit oikein annettu. 

Vertaustähtien valinnassa pitää lisäksi olla tarkkana, että mitattava kohde varmasti on vertaustähtien muodostaman kolmion sisäpuolella eikä mikään kolmion kulmista saisi olla kovin tylppä. Ainakaan ScanIt ei ole kovin tarkka, jos jokin em. ehdoista ei toteudu.

Vaikka itse kehun, PcCalculaattori on paras taskulaskinohjelma, mitä netistä löytyy.
Sen voitte ladata tuolta. Vaatii kylläkin tietokoneen näppäimistön.

Tarkuutta vaativissa mittauksissa vertaustähtien koordinaatteihin on tehtävä myös tähden ominaisliikkeestä aiheutuva korjaus, jos käytetyssä tähtiluettelossa sellaiset on annettu. Esim. tähden SAO 113387 ominaisliike RA:ssa on -0.0014 sek/vuosi  ja epookki 1937.5 mistä korjaus lasketaan havaintohetkeen. Jos googlen kuva olisi otettu esim. juuri nyt, olisi korjaus (2021,3-1937.5)*(-0.0014)/3600 = -0.000033 tuntia.

Lopuksi vielä tuo otsikon haaste. Hyväksyn bongaukseksi myös, jos löydätte Nurmen tuosta ao. simulaatiosta ja kerrotte, kuinka paljon sen paikka eroaa lasketusta paikkasta syyskuun 1. päivänä vuonna 2021 klo 0.0 UTC. 

Paavo Nurmi simulaatiossa 1.9. 2021 UTC 0.0.  Kuva EZGIF

Tarkkasilmäiset varmaan ovat jo löytäneetkin  Nurmen tuosta  blink komparaattorin simulaatiosta. Sen paikan voisi myös mitata edellä esitetyllä tavalla mutta tässä haasteessa riittävän tarkkuuden saa, jos kuvaa  vain suurentaa ja vertaa sitten paikkaa vastaavaan kohtaan hyvässä tähtikartassa (voipaperi on tässä hyvä apuväline).

Kuvan voi myös ladata CThruView  ohjelmaan, jonka avulla sitä voi säätää ja asemoida sen läpinäkyvänä tarkasti tähtikartan päälle. Ohjelmalla saattoi aikaisemmin myös klikata alla olevaa ohjelmaa mutta tämä ominaisuus ei nykyisin enää toimi. Sen sijaan kursorilla voi edelleen osoittaa haluttua kohtaa ja siirtyä sitten kartalle näppäinyhdistelmällä Alt+Tab. Kursorin paikka säilyy siirrossa ennallaan, mistä kartta voi  sen koordinaatit nyt  lukea. 

PS.

Lisähaasteena voisitte etsiä tähtitornin, jonka virallinen koodi on 99. Vihjeenä Iso-Heikkilä on 62 ja Kevola 64. Ja haastakaa myös kaverinne, laitetaan haaste kiertoon.

Making a telescope mirror by casting

If a liquid-filled vessel is rotating, the liquid rises at the edges and forms a pit in the center. If the axis of rotation is exactly vertical, the shape of the pit is a paraboloid, whose radius of curvature is

( 1 ) R = (946 / ω) ², where ω = rotational speed.

In the formula,  the quality of R is mm, if the rotational speed is in rpm. If, for example, ω = 33.3, becomes R = 806 mm, which would be suitable for an  amateur telescope and easy to implement even with a turntable, for instance.

I started my own experiments a couple of years ago when I quickly realized that the most difficult part of the job was the precise erection of the axis of rotation. Turntables usually have a suspension designed to reduce the effects of vibration. However, such a structure is not suitable for rotating a liquid surface but must be made completely fixed and a separate tilting plane must be built under the player to erect the turntable. Below is a picture of my solution.

Figure 1. Epoxy mold rotation mechanism.

The hardware store spirit level shown in the picture was only suitable for rough installation of the player. The final erection was done with a precision level with a scale spacing of 10 ". Note the lowest stack of discs stacked on top of the player. Its purpose was to stabilize the flap seen on the disc shaft. Over the stack is the epoxy mold and a cover to prevent dust and bugs from falling.

The entire treatment was assembled on a wall-mounted sauna bench. This was because  on the wooden floor  the player tilted + -25"  depending on where the  operator was standing. This problem was not present in the sauna but  there the stability of the benches became a problem. At the start of the casting. the  erection error  was always below  +-1" but at the end, when  the casting had dried, it typically was + -10 "in the depth  and + -30" in the width direction.

Epoxy resin

The casting plastic, epoxy,  was ordered from the net,  where the suppliers  can be found in the darkest of clouds. My choice fell on a company called  LI HSI TECH CO., LTD  because they had a good website and because they were also able to supply small test samples (1 kg). The choice was successful because the company's representative proved to be well acquainted with his field and willing to serve even small customers who may not know what they want. The range of epoxies available was large and customized for many different purposes. The differences between the substances are e.g. in their color, strength, viscosity and drying time.

After a few pilot lot on the advice of the company representative,  the products  E-0001 and H-0001 (epoxy and hardener) were found good, They flow almost like  water  and  dry surface dry in less than 20 hours.

Figure 2.  LIHSI   epoxy resin and  the mixer.

Mixing resin and hardener is then already its own art form, of which the web offers many good performances. Mine is that   Mixing epoxy resin. With different substances, the mixing ratio varies but on my own, it was 1: 3. However, that relationship was not critical. If there was too much hardener, the mixture would only dry faster and vice versa. In my own experiments, the drying time was at most 2 days, when the mixture was a bit lean when the substance ran out. However, it eventually became hard too.

It is important for mirror making that the mixture retains the shape it has acquired during its initial rotation during drying. If the layer to be cast is strong, this will not succeed because during mixing the mixture heats up and then gradually cools as it dries. Through the heel, I learned that the first casting will never succeed. You have to cast first a casting base, on top of which you have to pour another thin layer. A suitable layer thickness appeared to be about 2 mm. It might work even thinner, but I didn't have time to try that when the substance ran out.

Test specimens

The first test piece was a lousy attempt, whose purpose was only to test the casting technique. The mold was a small plate, which was rotated at 45 rpm. Although the surface was visibly bad,  it was Al-coated to see if  that is possible and indeed, it succeeded well.  The surface became very shiny, just like coated on glass,

Next, I tried to cast a small off-axis mirror - that is, one where the optical axis of the surface does not pass through the center of the mirror. However, this attempt failed because there was too little material  and  everything flowed to the outer edge  of the mold,  leaving the  inner edge incomplete. I had  calculated the epoxy demand assuming  the axis of rotation was in the middle of the mirror!

Figure 3 below shows two other exemplars, which succeeded better and are still without coating.

Figure  3. Reflections from uncoated blanks

The blank in the picture's green box  remained the best in this series of experiments. It has two additional 2 mm layers cast on top of the  first base (360 g), the lowest of which contains E55 g + H25 g and the second E60 g + H20 g.

The radius of curvature of the bottom was not measured, but on the  second layer, it was R = 800 mm and on the third R = 781 mm. When the diameter of the box is 212 mm, the aperture ratio would be f / 1.8, which is a very respectable value. However,  from figure 3 we can see that the reflection image is not good up to the edges, but must be cut at least 13 mm away from it. To be on the safe side, I limited it even more, leaving the final aperture ratio to  f / 2.1

On a black plate (Fig. 3), the radius of curvature  was    R = 750 mm, corresponding  ω= 34.5 rpm in  equation 1. Later I sawed off its center pin, which was an error. When sawing, the surface became hot and the reflection image clearly deteriorated. The new value of the radius of curvature became R = 672 mm. A similar but minor defect also occurred on the surface of the green box when I drilled 4 holes in the bottom for gluing the mounting screws.

Mirror testing

The easiest way to test a telescope mirror at home is to look at the image of the point light source it forms in different positions of focus. With a flawless mirror, the image is sharp in focus and a round plate evenly illuminated in extra or infrared. If a bright dot appears in the center of the plate in one position and a rounder ring in the other, either an over- or under-corrected spherical aberration is defective. However, if there are rings visible, the mirror is not hopelessly bad but is at least suitable for burning glass.

Below are the focus images of the mirrors in Figure 3. The light source was a small hole punched in aluminum foil which was reflected on  white cardboard next to the light source and photographed there.

Figure  4. Focusing images of good and bad mirrors.

The picture shows that the spherical aberration of the mirror in the green box  is slightly overcorrected but no coma or astigmatism can be detected from it.  However, the larger extra and infrafocal images in the upper corners  show that the mirror has small local defects, some of which form a similar pattern to the boreholes in Figure 3. The final epoxy layer was not thick enough to level evenly over these holes.  As expected, the surface of the black plate was so poor that it was not worth coating.

Experiment Telescope

The next step in testing was to use it in the right shooting situations. When there was no ready-made telescope for that purpose, one had to be quickly assembled. The end result is in the pictures below.

Figure 5.

Figure 6.

The telescope is built into a fairly sized cardboard tube from Biltema, supported by a shaky camera stand. Pictures are taken with a standard digital camera with an achromatic proximity lens. The finder is a pill tube pierced from the bottom, with a reticle formed of white sewing thread at the mouth. Illuminated with a flashlight, the tube opens up a really sleek sight that is precise enough to bring the subject into the camera’s field of view. There is still a carrying handle at the bottom of the tube and the adjusting screw knobs for mirror orientation.

The camera's optics can also be zoomed moderately, the only difficulty being that camera's automation tends to focus on the wrong subject and does not work in the dark at all.
Below is a photo, taken through three window panes, the accuracy of which, even with defects, is surprisingly good and clearly exceeds the expectations set at the beginning. By avoiding the slips described above, the result would undoubtedly be even better. Hopefully, some of the readers will take the challenge and  makes a better one.

Figure 7. Blackbird in a yard tree. In marked areas  image resolution is poor.

Photos, more in Finnish

Links:

Peilintekoa valamalla

Solar tracking sundial with three hands

Here are some archive photos from my former  solar tracking sun dial project.

Prototype

The driving mechanism was built from old children toys. As a time dial serves a small table clock.
Some Lego parts were used to clutch it into a 24 teeth worm gear which again was made of some BILO parts. Between the motor and the worm gear there is still a 1:3 gear and a 1:20 Lego gearbox.

25.02.2010 First time in outdoors

Tracker sensors - XOB17 solar cells

Panels W and E are used to track, panel S senses, if  sun is shining. If not, tracking is stopped.

Voltage compararor LT1017  drives the motor forward, if the  sensor W voltage > E.
Manual switch is used to drive the motor backwards.

Final version

Final version 2012.01.25

Driving mechanism

Clock dial connection

Original clips of the YouTube video

Clip 1   Clip 2   Clip 3   Clip 4   Clip 5   Clip 6